Arsip Bulanan: November 2014

Selalu Ada Pilihan

Hai! Apa kabar? Maafkan saya yang minggu lalu harusnya mengisi blog ini tidak berhasil menyelesaikan tugasnya dengan baik. Sedang banyak hal yang perlu dikerjakan dan dipikirkan.

Di antara sekian banyak pikiran tersebut, sebagian yang mengganggu saya adalah kebimbangan dalam keputusan yang harus diambil dari sekian banyak pilihan. Terkadang ada yang sudah jelas dengan konsekuensinya, tapi ada juga yang masih serba kelabu. Sadar atau tidak, pengambilan keputusan yang kita lakukan selalu dipengaruhi oleh pengalaman kita yang telah lalu.

Well, kali ini, topik yang akan diulas adalah mengenai pengambilan keputusan, terutama dalam hal membeli sesuatu. Bayangkan kasus seperti di bawah ini.

Di suatu malam yang indah, Anda pergi ke bioskop bersama sang kekasih untuk menonton premiere sebuah film sequel yang lama Anda tunggu-tunggu. Rasanya tapi ada yang kurang kalau tidak ada kudapan yang menemani menonton. Nah, akhirnya Anda memutuskan untuk membeli popcorn di gerai yang ada dalam bioskop tersebut. Ada tiga pilihan ukuran dengan tiga pilihan harga yang berbeda. Yang mana yang Anda pilih?

Aha!

Aha!

100 Lemparan Koin: Matematis

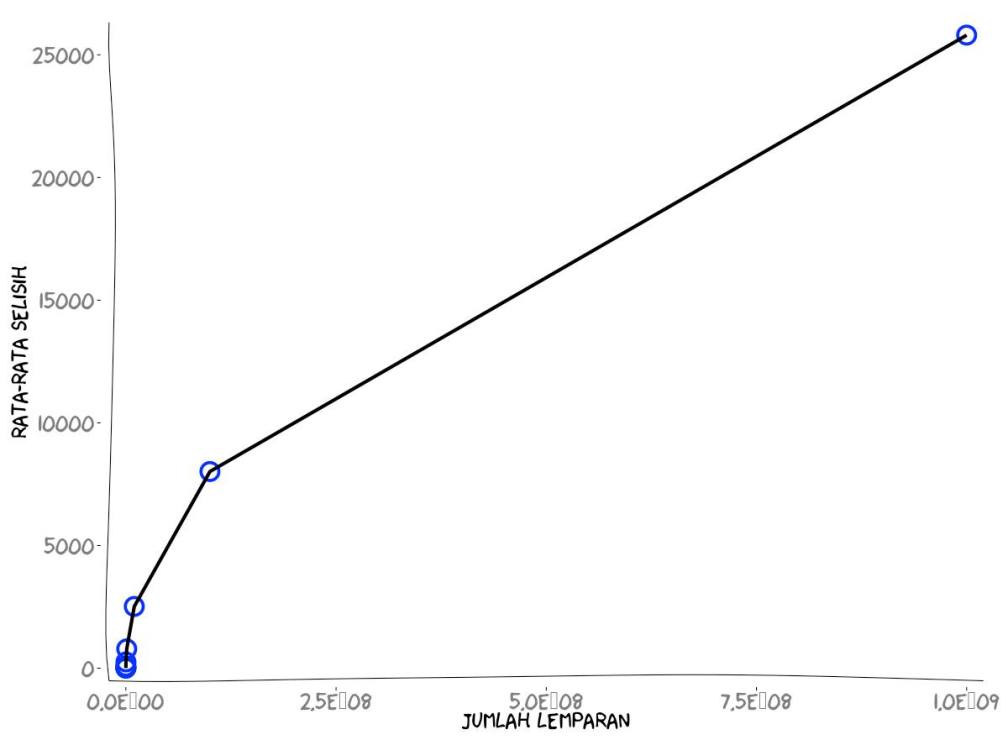
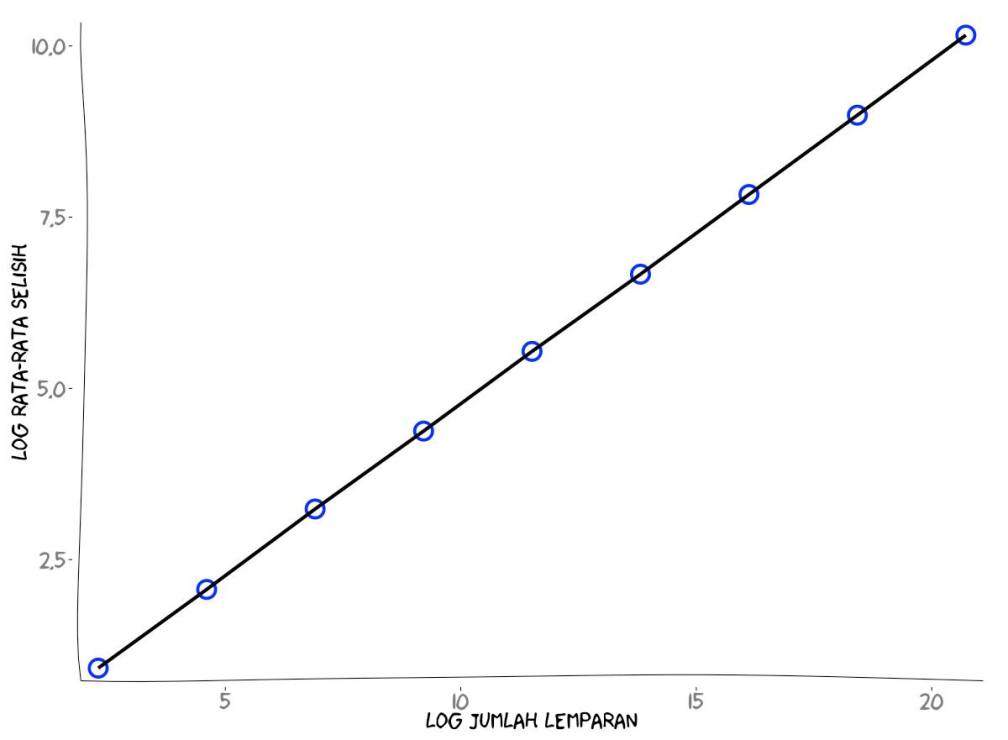
Minggu lalu kita sudah membahas simulasi 100 lemparan koin untuk menentukan rata-rata selisih kemunculan sisi muka dan belakang. Dalam artikel ini, kita akan menelaah secara matematis bagaimana memperoleh rata-rata tersebut, dan membandingkannya dengan hasil simulasi.

Kita nyatakan jumlah lemparan koin sebagai n, jumlah kemunculan sisi muka sebagai h, dan jumlah kemunculan sisi belakang sebagai t. h bisa bernilai antara 0 (sisi muka tidak muncul sama sekali) sampai dengan n (sisi muka selalu muncul). Kita ingin mengetahui rata-rata untuk d = |h – t|. Untuk contoh sederhana, perhatikan tabel berikut (n = 3):

Hasil lemparan h t = n – h d = |h – t|
HHH 3 0 3
HHT 2 1 1
HTH 2 1 1
HTT 1 2 1
THH 2 1 1
THT 1 2 1
TTH 1 2 1
TTT 0 3 3

Satu poin penting bisa kita cermati dari tabel di atas: jawaban rata-rata ~0 jelas salah. Mengapa? Perhatikan bahwa nilai terkecil d adalah 0 untuk n genap (yaitu jika h = t) dan 1 untuk n ganjil (yaitu jika h = (n – 1)/2 atau h = (n + 1)/2). Secara intuitif, kita tahu bahwa rata-rata dari sekumpulan bilangan yang seluruhnya lebih besar dari atau sama dengan 0 pasti lebih besar dari 0. Dengan demikian, rata-rata D juga pasti lebih besar dari 0. Perhatikan bahwa kita menulis d untuk nilai / konstan tertentu (misalnya d = 1) dan kita menulis D untuk menyatakan variabel acak yang sedang kita amati.

Lalu, berapa rata-rata D untuk sembarang n? Sebelum menjawab pertanyaan ini, mari kita konstruksi fungsi distribusi untuk D dengan terlebih dahulu membahas distribusi binomial.

Distribusi binomial

Distribusi binomial mendeskripsikan peluang sejumlah h “keberhasilan” (success) dalam n “percobaan” (trial) independen (baca: satu kejadian tidak akan mempengaruhi kejadian lainnya), dengan peluang keberhasilan pada masing-masing percobaan = p. Dalam kasus melempar koin, keberhasilan yang dimaksud adalah kemunculan sisi muka, dan satu percobaan sama dengan satu lemparan koin. Untuk koin seimbang, p = 0.5.

Distribusi binomial diekspresikan dalam persamaan berikut:

P(H=h|n,p)=\binom{n}{h}p^{h}(1-p)^{n-h}

Persamaan di atas menyatakan peluang kemunculan h sisi muka dalam n lemparan koin dengan peluang kemunculan sisi muka pada setiap lemparan p. 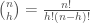\binom{n}{h} = \frac{n!}{h!(n - h)!} menyatakan jumlah kombinasi h sisi muka dalam n lemparan. Contohnya, dari tabel di atas kita tahu bahwa ada 3 kombinasi h = 2 untuk n = 3, yaitu HHT, HTH, dan THH.

Kemudian, ph(1 – p)n – h menyatakan peluang mendapatkan kombinasi tertentu. Contohnya, untuk kombinasi HHT peluangnya adalah p2(1 – p): p2 untuk mendapatkan dua H dan (1 – p) untuk mendapatkan satu T.

Untuk koin seimbang, karena p = 1 – p = 0.5, persamaan di atas dapat disederhanakan menjadi:

P(H=h|n,0.5) = \binom{n}{h} \frac{1}{2}^{h} \frac{1}{2}^{n - h} = \binom{n}{h} \frac{1}{2}^{n}

Sebagai contoh, berapa peluang kemunculan 2 sisi muka dalam 3 kali lemparan?

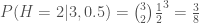
P(H=2|3,0.5) = \binom{3}{2} \frac{1}{2}^{3} = \frac{3}{8}

Periksa kembali bahwa 3/8 sama dengan jumlah kombinasi kemunculan 2 sisi muka dibagi total jumlah kombinasi pada tabel di atas.

Distribusi selisih muka-belakang

Sekarang kita akan memetakan distribusi binomial ke distribusi selisih muka-belakang. Perhatikan fungsi yang memetakan jumlah kemunculan sisi muka h ke selisih kemunculan kedua sisi d:

d = |h - t| = |h - (n - h)| = |2h - n| = \begin{cases} 2h - n, & h \geq \frac{n}{2} \\ n - 2h, & h < \frac{n}{2} \end{cases}

Karena h, n, dan d adalah bilang bulat, maka untuk n ganjil nilai d selalu ganjil dan untuk n genap nilai d juga genap (mengapa?).

Dari persamaan di atas, diketahui bahwa setiap nilai d bisa berasal dari dua nilai h, yaitu:

h = \frac{n + d}{2} atau h = \frac{n - d}{2} = n - \frac{n + d}{2}

Pengecualian berlaku untuk d = 0, yang hanya bisa diperoleh pada kasus n genap dan h = n/2.

Berdasarkan pemetaan dari d ke h di atas, diperoleh:

\begin{array} {lcl} P(D=d|n, 0.5) & = & P(H=\frac{n + d}{2}|n, 0.5) + P(H=n - \frac{n + d}{2}|n, 0.5) \\ & = & \binom{n}{\frac{n + d}{2}}\frac{1}{2}^{n} + \binom{n}{n - \frac{n + d}{2}}\frac{1}{2}^{n} \end{array}

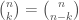Karena \binom{n}{k} = \binom{n}{n - k} untuk setiap n ≥ k, persamaan di atas dapat disederhanakan menjadi:

P(D=d|n, 0.5) = 2 \binom{n}{\frac{n + d}{2}} \frac{1}{2}^{n} = \binom{n}{\frac{n + d}{2}} \frac{1}{2}^{n - 1}

Untuk d = 0 dan n genap, 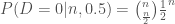P(D=0|n, 0.5) = \binom{n}{\frac{n}{2}} \frac{1}{2}^{n}.

Sebagai contoh, jika n = 3, probabilitas selisih jumlah kemunculan sisi muka dan belakang = 1 adalah:

P(D=1|3, 0.5) = \binom{3}{\frac{3 + 1}{2}} \frac{1}{2}^{3 - 1} = \frac{3}{4}

Rata-rata selisih kemunculan sisi muka dan belakang

Kita sudah mendapatkan fungsi distribusi untuk D. Secara umum, rata-rata suatu distribusi diskrit bisa dihitung menggunakan persamaan:

E[D] = \sum_{d}^{ }d\cdot P(D=d)

yaitu penjumlahan d dikali dengan peluang D = d, untuk setiap d dalam ruang sampel D. Contohnya, pada tabel di atas kita tahu bahwa jika n = 3, ruang sampel D (nilai yang mungkin untuk d) adalah 1 dan 3. Peluang D = 1 adalah 6/8 (6 baris dengan D = 1 dari total 8 baris), sedangkan peluang D = 3 adalah 2/8.

Lalu berapa rata-rata untuk D? Penulis sudah menurunkan rumus untuk menghitung rata-rata D dari persamaan di atas, yaitu:

E[D] = \begin{cases} n\binom{n}{n/2}/2^n, & n \, \, genap \\ (n + 1)\binom{n}{(n + 1)/2}/2^n, & n \, \, ganjil \end{cases}

Pembaca yang penasaran dengan penurunan rumus di atas dapat mengunduh dokumen ini.

Terakhir, mari kita jawab pertanyaan pada kuis kecil 2 minggu lalu.

Jika kamu melempar koin seimbang sebanyak 100 kali, berapa rata-rata selisih jumlah kemunculan sisi muka dan belakang?

Kita hanya perlu memasukkan n = 100 ke persamaan rata-rata di atas:

\begin{array} {lcl} E[D] & = & n\binom{n}{n/2}/2^n \\ & = & 100\binom{100}{50}/2^{100} \\ & = & 7,959 \end{array}

Jawaban yang kita peroleh dari simulasi kemarin adalah 7,963, hanya berbeda 0,004 dari perhitungan menggunakan rumus. Sangat dekat bukan?

100 Lemparan Koin: Simulasi

Jika kamu melempar koin seimbang 100 kali, berapa rata-rata selisih kemunculan sisi muka dan belakang? (Selisih yang dimaksud adalah nilai mutlak.)

Ketika diberikan pertanyaan kuis pertama kali oleh Bang Wibi, jawaban saya mungkin sama dengan kebanyakan dari para pembaca: ~0. Simpel saja alasannya toh? Kalau probabilitas munculnya muka dan belakang sama-sama 0,5, berarti kita bisa berharap bahwa selisihnya akan kecil sekali sehingga mendekati 0. Namun, kelihatannya jawaban tersebut tidak tepat, karena kalau terlalu mudah seperti itu, mengapa harus dibuat sebagai kuis?

Akhirnya, saya terpikir untuk membuat sebuah program simulasi. Perlu dibuat program yang dapat melakukan x kali simulasi untuk 100 lemparan koin sehingga bisa dihasilkan rata-ratanya. Bagusnya lagi, dengan begini kita juga bisa mendekati untuk n lemparan koin.

Sudah terbayang kira-kira programnya akan seperti apa?

Tenang saja. Bagi para pembaca yang lebih matematis, setelah artikel ini, akan disampaikan juga cara matematis untuk menyelesaikan masalah tersebut. Dengan begitu, kita juga bisa membandingkan perbedaan hasil dari simulasi dan hasil dari perhitungan matematis. Berikut saya lampirkan kode yang ditulis dalam bahasa Python untuk melakukan simulasi.

from random import randint

if __name__ == '__main__':
	flip = [10,100,1000]
	x = 10000

	for n in flip:
		s = 0
		for i in range(x):
			f = [randint(0,1) for j in range(n)]
			delta = abs((sum(f) - (n/2)) * 2)
			s += delta
		print float(s)/x

Catatan: Jangan keliru menafsirkan penamaan variabel ini dengan penamaan variabel yang digunakan di perhitungan matematis ya.

Nah, Bang Wibi sendiri ternyata juga melakukan simulasi. Namun, bahasanya berbeda (R), dan jumlah barisnya juga berbeda — lebih sedikit. Hasilnya memang akan berbeda. Bahkan dengan satu program yang sama, hasilnya juga selalu berbeda (karena keluaran dihasilkan berdasarkan hasil yang acak). Kode dengan bahasa R bisa dilihat di bawah ini.

n.trial

Hasil simulasi menunjukkan bahwa untuk 100 kali lemparan, didapatkan rata-rata selisihnya adalah 7,9628 dari 10.000 kali pengulangan. Angka ini berubah-ubah terus setiap simulasi, tapi tidak pernah di bawah 7 dan tidak pernah di atas 9. Ini menunjukkan secara empiris bahwa jawaban ~0 ternyata salah.

Pembaca boleh coba untuk membuat program yang serupa atau menjalankan program di atas dengan mengganti jumlah lemparannya. Perhatikan bahwa ketika lemparannya makin banyak, rata-rata selisihnya pun semakin besar! Kami cukup “kurang kerjaan” dengan membuat grafik dari hasil simulasi tersebut seperti yang dapat dilihat di bawah ini. Rata-rata diperoleh melalui 10.000 kali pengulangan untuk masing-masing 10, 100, 1.000, …, sampai 1 miliar lemparan koin. Kode sumber simulasi dapat diperoleh dari tautan ini.

Lemparan vs Selisih

Lemparan vs Selisih

Saya tidak begitu mengerti ini bentuknya mengikuti apa, tapi yang menarik adalah ketika grafik digambarkan dalam skala log-log, grafiknya menjadi linear!

Linear!

Linear!

Kira-kira mengapa bisa seperti itu ya?