Arsip Bulanan: Juni 2015

Simple Linear Regression – Bagian 2

Di pos sebelumnya, kita sudah membahas tentang regresi linear. Nah, kali ini kita akan membahas bagaimana mengevaluasi model yang sudah dihasilkan oleh regresi linear tersebut. Dengan kata lain, seberapa “akurat” model yang kita hasilkan dalam memprediksi titik-titik data yang ada.

Evaluasi Akurasi Perkiraan Nilai Koefisien

Selalu ada galat ketika melakukan estimasi terhadap nilai koefisien dan menentukan fungsi regresi yang digunakan. Entah karena ketidaksesuaian fungsi regresi yang digunakan (diasumsikan linear, padahal kuadratis, misalnya), adanya data pencilan, atau karena adanya pengaruh variabel lain yang belum dimasukkan sebagai pertimbangan untuk menyusun model regresinya. Oleh karena itu, fungsi linear yang didefinisikan sebelumnya dapat ditulis ulang sebagai

y = a + bx + \epsilon

dengan \epsilon adalah penampung dari semua hal yang mungkin kita lewatkan saat melakukan estimasi. Dalam kasus taksi yang digunakan pada pos yang lalu, contohnya adalah waktu tunggu taksi atau kesalahan pengukuran — ternyata argonya sedang rusak sehingga kita bayar seikhlasnya saja.

Nah, kita perlu mengingat bahwa data yang kita gunakan dalam memperkirakan nilai koefisien ini merupakan sekelompok sampel — bukan populasi. Oleh karena itu, dikenal lah benda-benda bernama confidence interval dan p-value yang digunakan untuk mengetahui apakah parameter yang digunakan untuk memprediksi y (nilai a dan b) itu signifikan atau hanya kebetulan saja. Walakin, beberapa orang sudah meninggalkan confidence interval dan p-value dewasa ini. Sedikit gambaran mengapa nilai-nilai itu ditinggalkan bisa dilihat di artikel ini dan komik ini.

Evaluasi Akurasi dari Model

Ada beberapa cara yang dapat digunakan untuk mengevaluasi model (fungsi) yang sudah dihasilkan. Intinya, kita ingin melihat seberapa jauh model yang kita hasilkan cocok dengan data yang tersedia. Berdasarkan kitab kuning ilmu statistik [1], ada dua metode yang secara umum dilakukan untuk mengevaluasi model yang dihasilkan: residual standard error (RSE) dan R^2. Sebagai tambahan, dalam pos ini akan diberikan juga metode evaluasi lainnya: root mean squared error (RMSE).

Residual Standard Error

Ingat bahwa di bagian sebelumnya sempat dibahas tentang munculnya \epsilon? Nah, RSE ini adalah estimasi simpangan baku (standard deviation) dari \epsilon. Rumus dari RSE dapat dituliskan sebagai berikut

RSE = \sqrt{\frac{1}{n-2} RSS} = \sqrt{\frac{1}{n-2} \sum_{i=1}^{n}(y_i - \hat{y_i})^2}

dengan nilai \hat{y_i} adalah prediksi nilai y ke-i berdasarkan model yang telah dibuat. Mengapa dibagi n-2? Karena n-2 adalah derajat kebebasan, dan dengan mengestimasi nilai \alpha dan \beta, maka kita sudah membuang dua derajat kebebasan. Artinya, semakin banyak parameter yang digunakan, maka semakin banyak pula nilai error yang dikompensasi.

R²

Sementara RSE hanya mengandalkan selisih dari nilai yang diprediksi dan nilai yang diobservasi, R^2 mencoba mengenalkan total sum of squares (TSS) yang mengukur ketersebaran dalam datanya sendiri. TSS diformulasikan sebagai TSS = \sum{(y_i - \overline{y})^2}, dan nilai R^2 dirumuskan sebagai

R^2 = \frac{TSS - RSS}{TSS} = 1 - \frac{RSS}{TSS}

Nilai R^2 yang mendekati 1 berarti data yang cukup bermacam-macam itu sudah tertangani dengan baik dalam model regresi linear yang dibentuk. Sedangkan jika nilai R^2 mendekati 0, maka kemungkinan model linear yang dibentuk tidak tepat, atau variansi dari datanya terlalu tinggi, atau keduanya.

Root Mean Squared Error

Terakhir, cara yang juga biasanya digunakan untuk mengevaluasi model regresi linear adalah dengan RMSE. Cara ini juga dikenal dengan nama root mean squared deviation (RMSD). Seperti dapat diperkirakan dari namanya, RMSE atau RMSD dihitung dengan menguadratkan error (predicted – observed) dibagi dengan jumlah data (= rata-rata), lalu diakarkan. Secara matematis, rumusnya ditulis sebagai berikut

RMSE = \sqrt{\frac{1}{n} \sum_{i=1}^{n} (\hat{y_i} - y_i)^2}

yang sebetulnya juga bisa dilihat sebagai

RMSE = \sqrt{\frac{1}{n} RSS}

Nah, dengan gambaran tersebut, semoga Anda sudah bisa lebih memahami gambaran mengenai simple linear regression. Untuk bagian berikutnya, kami akan mencoba memberikan contoh kode program untuk regresi linear. Sementara itu, selamat mencoba-coba!

—

Referensi
[1] James, G., Witten, D., Hastie, T., & Tibshirani, R. (2013). An Introduction to Statistical Learning (p. 68). New York: Springer.

Tiga Subjek yang Sebaiknya Kamu Pelajari Sebelum Kuliah S2 Pembelajaran Mesin

Dua, tiga bulan lagi kalendar akademik tahun ajaran baru akan dimulai. Bagi mereka yang akan kuliah, sepertinya waktu-waktu ini sangat pas dialokasikan untuk persiapan menghadapi perkuliahan. Di samping persiapan administrasi kuliah dan tempat tinggal (untuk yang berkuliah di luar kampung halaman), ada baiknya kita juga mempersiapkan otak kita agar nantinya lebih mudah menyerap materi kuliah. Salah satu caranya yaitu dengan mengulas (ulang) subjek-subjek yang relevan dengan materi kuliah. Walhasil, harapannya kita bisa lebih fokus mempelajari apa yang disuguhkan dosen di kelas, ketimbang sibuk mengejar ketertinggalan materi yang seharusnya sudah kita kuasai sebelum kuliah dimulai (prerequisites).

Dalam artikel ini penulis akan mencoba memberi tips tentang subjek apa saja yang menurut penulis paling membantu mengikuti kuliah S2 pembelajaran mesin. Dengan gaya hipwee. Mungkin pembaca berpikir, “Oh, pasti subjeknya tentang algoritma atau ngoding” atau subjek-subjek ilmu komputer lainnya. Hmm, meskipun tentunya ilmu komputer dan kemampuan menulis program tidak bisa kita abaikan, setidaknya ada 3 subjek lain yang sangat sangat krusial dalam kuliah pembelajaran mesin. Dan ketiganya berasal dari ranah matematika.

Apakah ketiga subjek itu?

Probabilitas dan Statistika

Yang pernah mendalami pembelajaran mesin pasti tahu bahwa yang menjadi dasar dari berbagai algoritma pembelajaran mesin adalah prinsip-prinsip probabilitas dan statistika. Prinsip itu ada di mana-mana! Mulai dari regresi, klasifikasi, pengelompokan, hingga yang paling mutakhir, deep learning.

Konsep sebaran probabilitas, misalnya distribusi normal, merupakan komponen utama dalam berbagai model supervised learning, di antaranya dalam model regresi linear dan model Naive Bayes. Konsep variabel acak berkaitan langsung dengan fitur atau dimensi dalam pembelajaran mesin, dan independensi antar variabel acak juga kerap dijadikan asumsi pemodelan. Contohnya, rantai Markov berasumsi bahwa nilai variabel saat ini (Xt) bergantung hanya pada nilai variabel tersebut pada waktu sebelumnya (Xt-1), alias independen terhadap nilai variabel pada waktu-waktu yang lebih lampau (Xt-2, Xt-3, …, X0).

Konsep lain dari probabilitas dan statistika yang tidak kalah pentingnya dalam pembelajaran mesin adalah konsep inferensi dan estimasi parameter. Misalnya dalam regresi linear (maafkan saya regresi linear, kamu sudah saya abuse sebagai contoh), kita ingin mengestimasi parameter regresi, yaitu parameter w0, w1, …, wp untuk variabel 1,…, p dan intercept. Bagaimana caranya? Salah satunya dengan metode maximum likelihood estimation (MLE). Usut punya usut, jika parameter regresi diestimasi dengan MLE, hasilnya menjadi ordinary least squares regression (OLS). Menariknya, metode estimasi yang berbeda untuk model yang sama bisa menghasilkan nilai parameter yang berbeda. Metode estimasi maximum a posteriori (MAP), yang merupakan metode Bayesian, akan menghasilkan ridge regression.

Masih banyak lagi contoh terapan estimasi parameter dalam pembelajaran mesin, dan masih sangat banyak lagi konsep probabilitas dan statistika yang dimanfaatkan dalam pembelajaran mesin. Kalau kamu hanya punya waktu untuk mengulas satu subjek sebelum memulai kuliah S2 pembelajaran mesin, penulis sarankan untuk memprioritaskan probabilitas dan statistika. Tidak perlu khawatir jika model-model yang dicontohkan di atas terdengar asing; jika kita menguasai prinsip probabilitas dan statistika, seharusnya tidak terlalu sulit untuk bisa memahami model-model tersebut.

Belajar dari mana: Dengar-dengar kuliah Harvard Stat110: Probability sangat bagus untuk belajar probabilitas (dan statistika), baik untuk pemula atau yang sudah lumayan berpengalaman. Demikian juga dengan teks yang digunakan dalam kuliahnya: Introduction to Probability.

Aljabar Linear

Kapan sih kita berhadapan dengan problem pembelajaran mesin yang hanya berkutat dengan 1 variabel bebas? Sepertinya jauh lebih mudah ya kalau cuma ada 1 variabel bebas (tentu ada beberapa pengecualian, misalnya untuk data deret waktu). Namun sayang sekali, hampir semua problem pembelajaran mesin berkaitan dengan data banyak variabel, termasuk data berupa gambar atau teks.

Di mana kita punya banyak variabel serta banyak poin data atau sampel, di situ kita menggunakan vektor dan matriks. Nah, vektor dan matriks ini dipelajari dalam cabang matematika yang dinamakan aljabar linear. Berbagai operasi terhadap vektor dan matriks dilakukan dalam komputasi pembelajaran mesin, mulai dari operasi aljabar, normalisasi, faktorisasi matriks atau reduksi dimensi, hingga kalkulus vektor dan matriks (yang dikenal juga dengan istilah kalkulus variabel banyak).

Sebuah dataset juga kerap direpresentasikan dalam bentuk tabel, yang ekuivalen dengan matriks. Masing-masing baris dalam tabel tersebut merupakan sebuah poin data, yang ekuivalen dengan vektor. Jika dimensi matriks adalah n baris x p kolom, atau n poin data dengan p variabel bebas, maka matriks atau dataset tersebut bisa dikonstruksikan ke dalam ruang p-dimensi, dengan tiap poin data menjadi sebuah titik dalam ruang. Lebih lanjut, kita bisa mentransformasikan matriks atau ruang p-dimensi tersebut sehingga dataset-nya menjadi lebih sesuai untuk model yang akan kita gunakan. Proses ini disebut feature engineering.

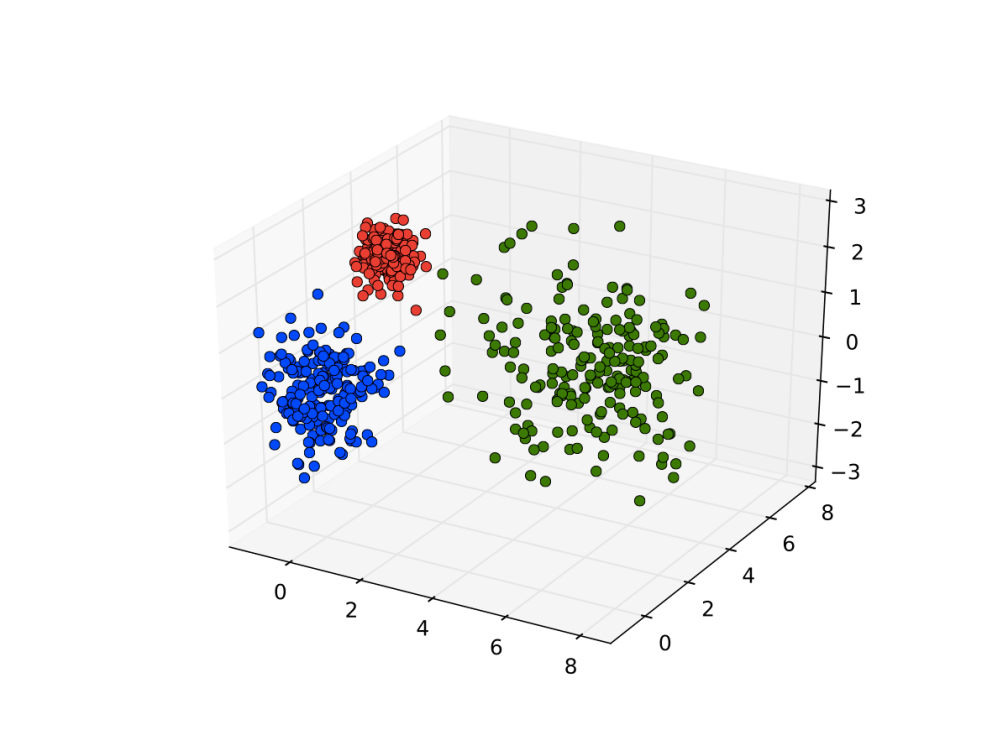
Representasi dataset dalam ruang p-dimensi

Contoh representasi dataset (matriks) untuk problem klasifikasi dalam ruang 3-dimensi. Warna poin data menyatakan kelas data tersebut. Gambar diambil dari solem’s vision blog

Aplikasi lain aljabar linear dalam pembelajaran mesin berasal dari sisi praktis, yaitu kemudahan penulisan atau notasi (notational advantage). Aljabar linear memungkinkan kita menulis fungsi dengan banyak variabel secara lebih mudah. Contohnya, bagaimana coba kita menulis probability density function dari distribusi normal multivariabel tanpa notasi matriks atau vektor? Selain kemudahan penulisan, banyak bahasa pemrograman yang mendukung operasi tervektorisasi, baik secara built-in maupun melalui pustaka. Operasi tervektorisasi ini umumnya lebih mudah untuk ditulis dan lebih natural untuk dibaca, ditambah lagi lebih cepat eksekusinya. Sering kali, operasi yang bisa ditulis dalam notasi vektor membutuhkan perulangan (e.g. for loop) jika ditulis tanpa notasi vektor. Contoh operasi perkalian matriks dengan dan tanpa vektorisasi bisa dilihat di sini.

Belajar dari mana: Kuliah daring MIT OCW 18.06: Linear Algebra banyak direkomendasikan untuk belajar aljabar linear, berikut buku yang ditulis oleh profesornya (Gilbert Strang): Introduction to Linear Algebra. Untuk kuliah yang lebih mendasar, terdapat 2 MOOC lain, yaitu Coding the Matrix di Coursera dan Linear Algebra – Foundations to Frontiers di edx.

Kalkulus

Kata siapa kamu tidak akan ketemu lagi sama kalkulus? Kalkulus itu ada di mana-mana. Paling tidak, kalkulus ada di kuliah S2 pembelajaran mesin.

Sebelumnya penulis sudah memberi contoh singkat estimasi parameter dengan MLE. Melalui MLE, dihasilkan parameter-parameter yang memaksimalkan fungsi likelihood (atau meminimalkan fungsi likelihood negatif), berdasarkan data yang kita miliki. Bagaimana cara memaksimalkan sebuah fungsi? Ingat-ingat kembali kalkulus atau matematika SMA. Ya, jawabannya adalah: diferensial. Banyak sekali problem pembelajaran mesin yang pada akhirnya bisa diformulasikan sebagai permasalahan optimasi, misalnya optimasi fungsi likelihood ataupun optimasi galat (contoh optimasi galat dalam regresi linear bisa dilihat di sini). Asumsinya adalah, jika terdapat suatu titik dalam range fungsi yang merupakan optimum global, maka secara teoretis parameter yang menghasilkan optimum global merupakan parameter “terbaik” untuk data yang kita miliki. Jika tidak ada optimum global, digunakan metode optimasi lain seperti gradient descent, yang juga memanfaatkan diferensial dalam komputasinya.

Tak terpisahkan dari diferensial adalah integral. Aplikasi integral dalam pembelajaran mesin terutama berkaitan dengan sebaran probabilitas dan probabilitas marginal. Misalnya, dalam metode Bayesian, probabilitas posterior P(Y | X) didefinisikan sebagai probabilitas gabungan P(X, Y) = P(X | Y) * P(Y), yang dinormalisasi (i.e. dibagi) dengan probabilitas marginal P(X). Biasanya kita hanya mengetahui rumus P(X | Y) dan P(Y). Bagaimana memperoleh rumus probabilitas marginal P(X) agar kita bisa menghitung probabilitas posterior P(Y | X)? Yaitu dengan memarginalisasi variabel Y dalam persamaan P(X, Y). Jika Y merupakan variabel kontinu, maka marginalisasi dilakukan dengan menghitung integral. Contoh lain pemanfaatan integral dalam pembelajaran mesin adalah pada model probabilistik grafis.

Selain diferensial dan integral, jangan lupa juga dengan dua fungsi yang sangat esensial dalam kalkulus: logaritma dan eksponen. Misalnya, logaritma dari fungsi likelihood sering digunakan untuk mempermudah komputasi optimasi, baik di atas kertas (ingat bahwa salah satu identitas logaritma adalah “memecah” perkalian) maupun di dalam komputer (untuk mencegah arithmetic overflow). Eksponen sendiri banyak ditemukan dalam sebaran probabilitas, dan ada “keluarga” distribusi khusus yang didasarkan pada fungsi eksponen. Konsep-konsep lain dari kalkulus seperti asimtot dan limit juga ada dalam pembelajaran mesin.

Belajar dari mana: Di Coursera ada 2 kuliah yang oke untuk belajar kalkulus: Calculus One dan Calculus: Single Variable. Untuk kalkulus variabel banyak, kita bisa belajar dari MIT OCW 18.02: Multivariable Calculus.

Selamat belajar dan selamat menjadi mahasiswa lagi!

Simple Linear Regression – Bagian 1

Ceritanya nih ya, dalam regresi itu kita ingin memprediksi angka suatu variabel y berdasarkan variabel-variabel lain X. Salah satu bentuk regresi yang paling sederhana adalah regresi linear sederhana. Seperti namanya, pada regresi jenis ini kita mencoba memperkirakan perubahan nilai y dalam suatu bentuk yang sangat sederhana: fungsi linear, yang secara matematis biasa dituliskan sebagai

y = a + bx

Oh, jangan merasa bingung dengan penulisan fungsinya ya. Variabelnya bisa saja ditulis dalam berbagai simbol di literatur yang Anda baca. Bisa saja tertulis sebagai

Y = \beta_0 + \beta_1X

atau mungkin

h_\theta(x) = \theta_0 + \theta_1x

Yang penting, persamaan tersebut menunjukkan bentuk fungsi linear. Supaya mudah — dan konsisten dengan pos sebelumnya, kita pakai representasi yang pertama.

Dalam artikel sebelumnya, contoh yang digunakan adalah perkiraan tarif taksi (y) dengan menggunakan jarak sebagai atribut yang digunakan (x). Saat menggunakan taksi, kita bisa melihat bahwa ketika kita baru masuk, argonya sudah menunjukkan angka 7500. Sehingga nilai a bisa kita substitusikan* dengan 7500.

Nah, nilai b kemudian bisa dicari setelah kita beberapa kali menggunakan taksi. Karena kita tahu jarak yang kita tempuh dan tarifnya, maka kita bisa jadikan itu sebagi sebuah sistem persamaan linear (SPL). Dari sana, kita bisa menggunakan cara yang mungkin selama ini cukup sering kita gunakan saat berhadapan dengan soal SPL dalam bentuk pilihan ganda: coba saja nilainya satu per satu. Dengan cara seperti itu, seharusnya kita bisa mendapatkan model regresi linear sederhana, meski tentu saja ada galatnya karena kita tidak menghitung kenaikan argo karena waktu tunggu — ketika taksi berhenti di lampu merah atau menghadapi macet, misalnya. Dari sanalah kemudian didapatkan bahwa nilai b adalah 15000.

Linear Regression with ErrorNamun, faktanya ternyata tidak semudah itu. Nilai a dan b — yang juga dikenal dengan nama “koefisien” atau “parameter” — acap kali tidak mudah untuk diketahui. Nah, seperti halnya mencari tarif taksi tadi, hal yang kita lakukan sebetulnya adalah meminimalkan galat atau error tersebut. Secara matematis, salah satu hal yang umum dilakukan adalah dengan menggunakan jumlah jarak terpendek dari kuadrat galat tersebut: residual sum of squares (RSS).

Nilai RSS diperoleh dengan melihat selisih dari nilai (dalam kasus ini adalah “tarif”) yang diprediksi (predicted; \hat{y}) — yang didapatkan dari model yang dibentuk (\hat{y} = a + bx) — dengan nilai hasil observasi (observed; y). Jadi, dapat ditulis sebagai

\hat{y} - y = observed - predicted = e

Nah, untuk setiap titik data yang ada (data ke-1 sampai data ke-n), dihitung nilai error-nya. Lalu, setiap nilai tersebut dikuadratkan, untuk kemudian dijumlahkan. Persamaan tersebut dapat ditulis sebagai

RSS = e_1^2 + e_2^2 + \cdots + e_n^2

yang ekivalen dengan

RSS = (y_1 - a - bx_1)^2 + (y_2 - a - bx_2)^2 + \cdots + (y_n - a - bx_n)^2

Dengan menggunakan ilmu sakti bernama kalkulus, didapatkan bahwa nilai a dan b yang meminimalkan galat (RSS) adalah

b = \frac{\sum_{i=1}^{n} (x_i - \overline{x}) (y_i - \overline{y})}{\sum_{i=1}^{n} (x_i - \overline{x})^2}
a = \overline{y} - b\overline{x}

dengan nilai \overline{y} dan \overline{x} adalah nilai rata-rata dari y dan x berdasarkan sampel yang diambil.

Nah, bagaimana caranya untuk mengevaluasi model yang sudah dihasilkan? Tunggu di pos berikutnya ya.

—

* Nilai a — seperti pada penjelasan di paragraf berikutnya — tidak selalu semudah itu ditemukan. Sebetulnya, nilai a — dan juga b — hampir selalu merupakan hasil estimasi.